作業中のメモ

よく「計算機」を使って作業をする．知らなかったことを中心にまとめるつもり．

Ubuntu 14.04 LTE の入力メソッド

Linux

どうも筆者です．

最近，仮想 OS に Ubuntu 14.04 LTE をインストールした． しかし，デフォルトの Unity では動作が重いため，Xubuntu を導入することにした．

Xubuntu の導入

Xubuntu 自体は，コマンド叩けば導入が出来た．

ところが，いつも通り日本語を入力しようとすると，直接入力と日本語入力が，高速に切り替わる状況となってしまった．すなわち，日本語を入力しようとしても，タイミングが悪いと直接入力になってしまい，直接入力に変更しようとしても，タイミングが悪いと日本語入力のままという状況になった．このままでは，使いづらいので，何とかする必要があった．

入力メソッドについて

まずは，入力メソッドについて調べた．すると，IBus や Fcitx，uim というものがあることが分かった．最近では，Fcitx が主に利用されているようである．

入力メソッドの確認

ここでは，自分の計算機が Fcitx になっているか調べるため，「設定」→「言語サポート」から，「キーボード入力に使う IM システム」の項目を調べ，fcitx となっていることを確認した． 次に，「設定」→「fcitx 設定」から，fcitx の設定を確認した．

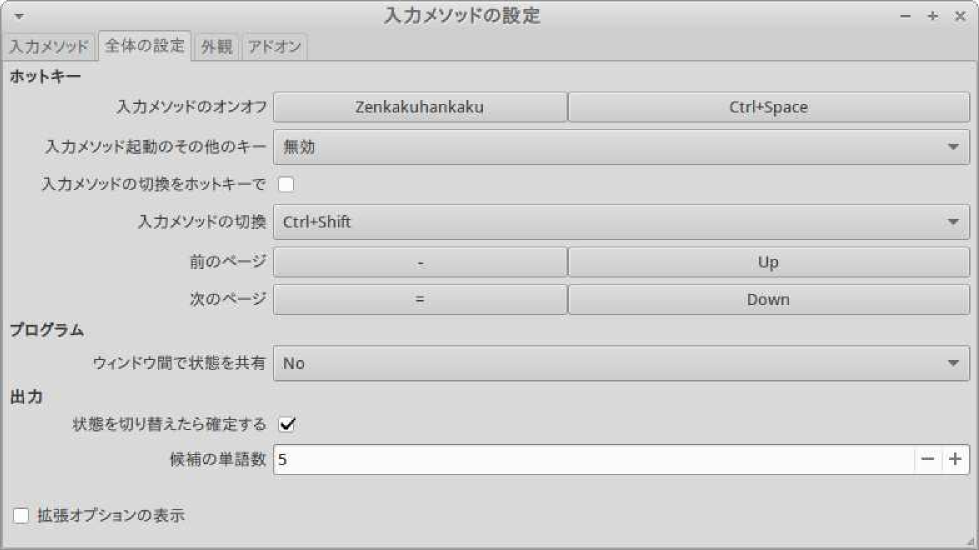
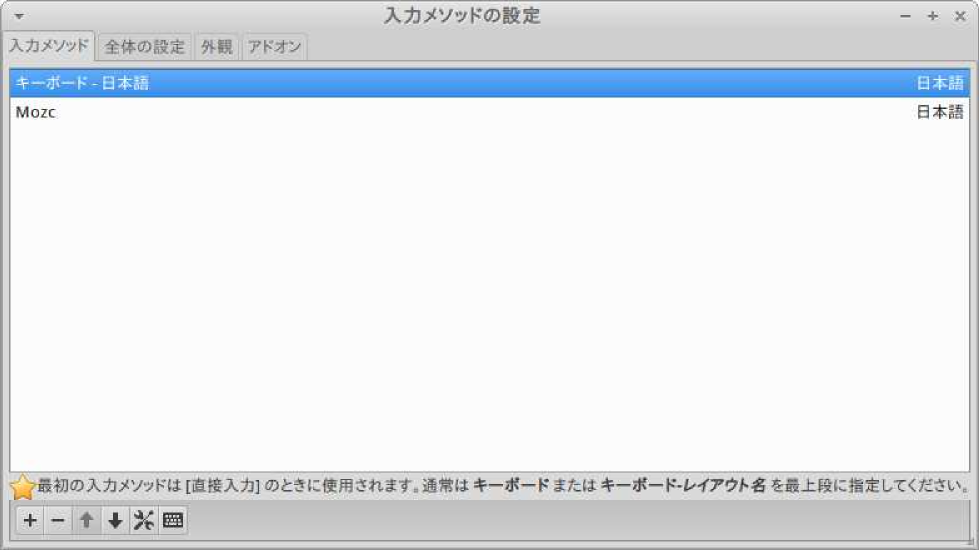
入力メソッドの設定内容

入力メソッドには，「日本語キーボード」と「Mozc」が設定されており，全体の設定では，Zenkakuhankaku と Ctrl + Space で，入力メソッドのオンオフが出来るようになっていた． 試しに，Zenkakuhankaku のキーを ESC キーで無効にしたところ，問題はなくなったが，Ctrl + Space で入力切替を行わないといけない状況になってしまった．コレでは不便である． そこで，どこかに設定ファイルがあると思い，探してみると，以下の場所にあることが分かった．

入力メソッドの設定ファイルの変更

設定ファイルの場所が分かったので，これを編集して設定を行う．まずは，ESC キーで切り替えが行えるようにした．

これで，荒ぶることなく切り替えが行えるようになったが，Vim を使用する筆者にとって，これでは少し不便であった．設定ファイルをもう少し見ていくと，インプットメソッドをオンにする時と，オフにする時のキーが別々で設定できることが分かった．

そこで，インプットメソッドをオンにするときは，半角/全角キーを，オフにするときは ESC キーを使うように設定を行った．

これで，荒ぶることなく，Vim に支障なく日本語と直接入力の切り替えが行えるようになった．

レーベンバーグ・マーカート法と準ニュートン法（C 言語）

プログラミング Linux

どうも筆者です．

最近，観測データを既知の関数で近似する必要が生じた．そのための近似方法を以前示したが，あれは，そのままプログラムを組むと，次元が大きくなると解きにくくなってしまうという問題がある． そのため，何か良い方法がないかと調べていたところ，「レーベンバーグ・マーカート法」というものがあることが分かった．

レーベンバーグ・マーカート法は，非線形関数の 2 乗和が最小になるものを求める方法として使われるらしい．これを使えば，誤差の 2 乗和が最小となるという点で，関数フィッティングが行える．

これを使うには，「LAPACK」と「BLAS」が必要になる．なので，参考サイトにあるように，インストールを試みたが，「levmar」が上手くインストール出来なかった．しかし，筆者の PC には，Intel コンパイラがインストールされている．このときに，MKL も一緒にインストールされるので，これを用いれば実行出来るのではないかと考えた．Makefile があったので，Intel 用の「Makefile.icc」を書き換えることにした．現段階では，バージョンが 2.6 であり，Makefile.icc の中身は，1 段目のようになっている．このまま使えば動くはずだったが，上手く動かなかった（f2c をインストールし忘れていたのが原因だと思う）ので，Makefile.icc を 2 段目のように書き換えた．

これで，実行することが出来た．ここで，[IntelVersion] は，各々がインストールした Intel Compiler のバージョンが記述されたディレクトリ名が入る．ここは，各自調べて欲しい．

また，関数の最小値も求めたかったので，色々調べた．すると，「liblbfgs」というパッケージが存在することが分かった．これは，Fortran で実装されていた「準ニュートン法」を C 言語に直したものらしい．よくやったなぁ．．．作者に感謝しつつ，手順に従ってインストールすることにした．しかし，これも何故かインストールが上手くいかなかったので，仕方なく，毎回コンパイルすることにした．

修正した Makefile とソースコートは以下のようになった．

また，ファイルの階層は，

  • Makefile [libsrc] [src]
    • [libsrc] 「levmar-2.6」に含まれているファイルを全てコピーし，Makefile を書き換えたもの．
    • [src] MT.h arithmetic_ansi.h lbfgs.c lbfgs.h main.c

という風になっている．分かりづらくて申し訳ない．

今回は，

 { \displaystyle 
  y = -2x^{2} + 6x + \dfrac{1}{2}
}

の最大値を求めることにした．真の関数値に ボックス・ミューラー法により，標準正規分布に従う乱数を加えたものを測定値とした．そして，

  1. レーベンバーグ・マーカート法により，測定データを 2 次関数で近似する．そのときのパラメータを p[0]，p[1]，p[2] とした．
  2. 近似したパラメータを用いて，準ニュートン法により，最大値をとる x を求めた．

という流れで処理を行った．最初は，levmar で実装されている「dlevmar_dif」の引数「adata」の使い方が分からなかったが，調べたところ，キャストして渡せばよいらしいので，プログラムにあるように渡した．また，これと似た関数に「dlevmar_def」というものがある．これは，ヤコビ行列を計算する関数を自分で与える場合に利用する．今回は，面倒だったので，近似したものを用いた（すなわち，dlevmar_dif を利用した）．

また，lbfgs では，float と double の使い分けが出来るようにしてあるため，double ではなく，「lbfgsfloatval_t」というものが利用されている．個人的には，double でしか計算しないので，ここは，double と書いてもかまわない（ヘッダーで typedef により宣言されているだけなので）．

dlevmar_dif には，ユーザー側が与えるデータとして，測定データを与えているのに対し，lbfgs では，推定した係数データを与えていることに注意．また，最小値を求める関数であるため，最大値を求める場合は，マイナスをかけておく必要がある．そのため，evaluate 関数では，最後に，g[0] と fx の符号を反転させている．

これを実行すると，p[0] = -2.002300，p[1] = 5.944318，p[2] = 0.611619 と係数を推定でき，最大値を取る x は， \hat{x} = 1.484373 と求められる．真の関数では， x^{*} = \dfrac{3}{2} のとき最大となるので，正しく推定できていることが確認できた．

参考文献

Levenberg-Marquardt in C/C++

http://kivantium.hateblo.jp/entry/20140408/p1

http://www.sat.t.u-tokyo.ac.jp/~omi/random_variables_generation.html#Prepare_MT

Windows 7 での画面出力の設定

Windows 雑記

お久しぶりです．筆者です．

最近，PC を買い換えた．最近のマザーボードには，DVI や HDMI のグラフィック出力機能が搭載されているんだな．進歩したものだ．

以前使用していた PC には，マザーボードにそういった機能がなかったため，グラフィックボードを購入して取り付けていた．今回は，以前購入したオンボードに加え，オンボードの出力も利用できることとなる． 筆者は今，デュアルモニタで PC を使用している．しかし，冬場の寒い時期や友達が来たときには，テレビ等に出力して作業をしたくなるときがある． そこで，必要なときにテレビに出力する方法を以前から考えていたが，たまにしか使わない機能のためにグラボを買い足すのに意味があるのか，と考えていた． 今回は，以前から考えていたことが実現できるのではないかと思い至った．

前置きが長くなったが，今回もたいしたことではない．ただ単に，Windows の知らなかった機能が知れたという報告だけである．

さて，実際にテレビにつなぐため，Amazon で HDMI ケーブルを購入し，配線を行った．BIOS 等の設定をして，グラボとオンボードの両方が使えるようにした（細かいことは，以下の URL を参考にした）．その後，ドライバー等の設定を行って，テレビに出力することに成功した．

成功はしたが，まだこの時期（設定したのは 10 月初め）は，そこまで寒くないので，テレビに出力することはほとんどない．しかし，比較的友達が遊びに来るので，平均して 2 週間に 1 回程度はテレビに出力していた．また，普段テレビも見るので，

  1. 友達が来て，必要になったら HDMI ケーブルをオンボード側につなぐ．
  2. パソコンを使いつつ，テレビもつけたくなったら，HDMI ケーブルを抜く．

ということを行っていた．ただ，これはかなり面倒な作業であって，個人的に，あまりプラグを抜き差ししたくなかった．また，最近は接続をする頻度が高くなっていたので，その度にいじらなければならなかった．

そこで，何か良い方法がないかと，今日調べた（遅い）．すると，流石は Windows，ソフトウェアを入れなくても欲しい機能がすでに備わっていた．「画面の解像度」の設定から，認識しているモニタの数を確認する．現段階では，PC 用のモニタ 2 台とテレビの合計 3 台であった．ここから，テレビの出力をしている（設定画面上の）モニタを選択肢し，「複数のディスプレイ」の部分に注目する．多くの場合は，「表示画面を拡張する」という風になっている．ここからプルダウンメニューの項目を見ると，「このディスプレイを切断する」という項目があることに気づいた．テレビに対してこの設定を行うと，テレビを見ていても HDMI の出力はされなくなりかつ，ケーブルを取り外さなくて良くなる．この機能を知ったときに筆者は感動した．

この機能のおかげで，ケーブルを抜き差しすることなく，システム上で出力の設定が「手軽に」行えるのである．PC をつけたたま，テレビを消すと，設定画面上からは消えてしまうが，再びテレビをつけたときに「検出」をしてやることで再び認識される．

普段，デュアルモニタで一方を表示させないような設定をしようとは思わないため，この機能に気付かなかった．このおかげで，得した気分になれた．

テレビに出力している人で，同じことを考えている人がいたら，ぜひ参考にして欲しい．ではでは．

参考文献

Z87-PRO：オンボード出力とグラフィックカード出力の同時利用（マルチディスプレイ）について

LU 分解による連立一次方程式の解法

プログラミング 数学

前回は，ガウスの消去法について，簡単に説明した．今回は，LU 分解について説明する．

LU 分解

行列 {A} は正則行列（逆行列を持つもの）であるとする．このとき，行列 {A} を部分ピボット選択をする（この行列を {P} とする）ことにより，

 { \displaystyle
  PA = LU
}

のように LU 分解できる．ここで，L，U はそれぞれ，

 { \displaystyle
  \begin{equation}
    L = \left(
      \begin{array}{ccccc}
        1 & 0 & 0 & \cdots & 0\\
        l_{2}^{(1)} & 1 & 0 & \cdots & 0\\
        l_{3}^{(1)} & l_{3}^{(2)} & 1 & \cdots & 0\\
        \vdots & \vdots & \vdots & \ddots & \vdots\\
        l_{n}^{(1)} & l_{n}^{(2)} & l_{n}^{(3)} & \cdots & 1\\
      \end{array}
    \right),\quad U = \left(
      \begin{array}{ccccc}
        a_{11}^{(0)} & a_{12}^{(0)} & a_{13}^{(0)} & \cdots & a_{1n}^{(0)}\\
        0 & a_{22}^{(1)} & a_{23}^{(1)} & \cdots & \cdots a_{2n}^{(1)}\\
        0 & 0 & a_{33}^{(2)} & \cdots & a_{3n}^{(2)}\\
        \vdots & \vdots & \vdots & \ddots & \vdots\\
        0 & 0 & 0 & \cdots & a_{nn}^{(n - 1)}\\
      \end{array}
    \right)
  \end{equation}
}

である．ここから， {A\boldsymbol{x} = \boldsymbol{b}} を解くことを考える．まず， {L \boldsymbol{y} = P\boldsymbol{b}} を解く．すなわち，

 { \displaystyle
  \begin{equation}
    \left(
      \begin{array}{ccccc}
        1 & 0 & 0 & \cdots & 0\\
        l_{2}^{(1)} & 1 & 0 & \cdots & 0\\
        l_{3}^{(1)} & l_{3}^{(2)} & 1 & \cdots & 0\\
        \vdots & \vdots & \vdots & \ddots & \vdots\\
        l_{n}^{(1)} & l_{n}^{(2)} & l_{n}^{(3)} & \cdots & 1\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        y_{1}\\
        y_{2}\\
        y_{3}\\
        \vdots\\
        y_{n}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        b_{p_{1}}\\
        b_{p_{2}}\\
        b_{p_{3}}\\
        \vdots\\
        b_{p_{n}}\\
      \end{array}
    \right)
  \end{equation}
}

を解くことになる．ここで， {b_{p_{k}}} は，部分ピボット選択により，入れ替えたものを表す．入れ替えが行われなかった場合は， {b_{p_{k}} = b_{k}} である． この方程式は，前進代入で解くことが出来る．つまり，

 { \displaystyle
  \begin{equation}
    y_{k} = b_{p_{k}} - \sum_{j = 1}^{k - 1} l_{k}^{(j)} y_{j},\quad (k = 1, \cdots, n)
  \end{equation}
}

で求められる．次に， {U \boldsymbol{x} = \boldsymbol{y}} を解く．すなわち，

 { \displaystyle
  \begin{equation}
    \left(
      \begin{array}{ccccc}
        a_{11}^{(0)} & a_{12}^{(0)} & a_{13}^{(0)} & \cdots & a_{1n}^{(0)}\\
        0 & a_{22}^{(1)} & a_{23}^{(1)} & \cdots & \cdots a_{2n}^{(1)}\\
        0 & 0 & a_{33}^{(2)} & \cdots & a_{3n}^{(2)}\\
        \vdots & \vdots & \vdots & \ddots & \vdots\\
        0 & 0 & 0 & \cdots & a_{nn}^{(n - 1)}\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
        \vdots\\
        x_{n}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        y_{1}\\
        y_{2}\\
        y_{3}\\
        \vdots\\
        y_{n}\\
      \end{array}
    \right)
  \end{equation}
}

を解く．これは，ガウスの消去法のときと同様に，後退代入で解くことが出来る．つまり，

 { \displaystyle
  \begin{equation}
    x_{k} = \dfrac{1}{a_{kk}^{(k - 1)}} \left( y_{k} - \sum_{j = k + 1}^{n} a_{kj}^{(k - 1)}x_{j} \right),\quad (k = n - 1, \cdots, 1)
  \end{equation}
}

で求められる．

アルゴリズム

これを，C 言語で書き下すと以下のようになる．

参考文献

ガウスの消去法，LU 分解 http://www.ms.u-tokyo.ac.jp/~narutaka/lec/lud.pdf

LU 分解法 http://www.kata-lab.itc.u-tokyo.ac.jp/OpenLecture/SP20121218.pdf

ガウスの消去法のプログラム

数学 プログラミング

前回は，関数近似を行うことを考えた．このとき，係数を求めるために，連立方程式を解く必要が生じた． 今回は，とりあえず，ガウスの消去法を用いて，連立方程式を解くことを考える．

ガウスの消去法

ガウスの消去法は，中学，高校のときに習った連立方程式の 1 つである消去法を用いる． ガウスの消去法では，行列表示された連立方程式の係数行列を上三角行列に変形（前進消去）し，今度は逆方向に解を求めていく（後退代入）という手法をとる．

例題

例えば，以下のような 3 × 3 の係数行列と右辺ベクトルから解を求めることを考える．

 { \displaystyle
  \begin{equation}
    \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        1 & 1 & -1\\
        1 & -2 & 3\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        4\\
        -1\\
      \end{array}
    \right)
  \end{equation}
}

この行列を上三角行列に変形したいので，まずは，1 列目に関して， {\dfrac{(2, 1)\mbox{成分}}{(1, 1)\mbox{成分}}} の値を計算し， 2 行目から {\dfrac{(2, 1)\mbox{成分}}{(1, 1)\mbox{成分}} \times \mbox{1 行目}} を引けばよい．そして，右辺ベクトルにも同様のことを行う．この場合， {\dfrac{(2, 1)\mbox{成分}}{(1, 1)\mbox{成分}} = \dfrac{1}{2}} であるので，

 { \displaystyle
  \begin{eqnarray}
    & & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        1 & 1 & -1\\
        1 & -2 & 3\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        4\\
        -1\\
      \end{array}
    \right)\\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        1 - \dfrac{1}{2} \cdot 2 & 1 - \dfrac{1}{2} \cdot 1 & -1 - \dfrac{1}{2} \cdot (-2)\\
        1 & -2 & 3\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        4 - \dfrac{1}{2} \cdot 1\\
        -1\\
      \end{array}
    \right) \\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        1 & -2 & 3\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        -1\\
      \end{array}
    \right) 
  \end{eqnarray}
}

となる．同様に， {(3, 1)} 成分に対しても計算を行う．この場合， {\dfrac{(3, 1)\mbox{成分}}{(1, 1)\mbox{成分}} = \dfrac{1}{2}} であるので，

 { \displaystyle
  \begin{eqnarray}
    & & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        1 & -2 & 3\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        -1\\
      \end{array}
    \right) \\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        1 - \dfrac{1}{2} \cdot 2 & -2 - \dfrac{1}{2} \cdot 1 & 3 - \dfrac{1}{2} \cdot (-2)\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        -1 - \dfrac{1}{2} \cdot 1\\
      \end{array}
    \right) \\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        0 & - \dfrac{5}{2} & 4\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        - \dfrac{3}{2}\\
      \end{array}
    \right)
  \end{eqnarray}
}

となる．次に，2 列目に対して，計算を行う．ここでは， {\dfrac{(3, 2)\mbox{成分}}{(2, 2)\mbox{成分}}} の値を計算し，3 行目 から， {\dfrac{(3, 2)\mbox{成分}}{(2, 2)\mbox{成分}} \times \mbox{2 行目}} を引く．ここでは， {\dfrac{(3, 2)\mbox{成分}}{(2, 2)\mbox{成分}} = -5} となるので，結果は，

 { \displaystyle
  \begin{eqnarray}
    & & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        0 & - \dfrac{5}{2} & 4\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        - \dfrac{3}{2}\\
      \end{array}
    \right)\\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        0 & - \dfrac{5}{2} + 5 \cdot \dfrac{1}{2} & 4 + 5 \cdot 0\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        - \dfrac{3}{2} + 5 \cdot \dfrac{7}{2}\\
      \end{array}
    \right) \\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & \dfrac{1}{2} & 0\\
        0 & 0 & 4\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        \dfrac{7}{2}\\
        16\\
      \end{array}
    \right) \\
    & \Leftrightarrow & \left(
      \begin{array}{ccc}
        2 & 1 & -2\\
        0 & 1 & 0\\
        0 & 0 & 4\\
      \end{array}
    \right)\left(
      \begin{array}{c}
        x_{1}\\
        x_{2}\\
        x_{3}\\
      \end{array}
    \right) = \left(
      \begin{array}{c}
        1\\
        7\\
        16\\
      \end{array}
    \right)
  \end{eqnarray}
}

となる．最後の処理は必要ないが，ここに書く上で，分数は記述が面倒であるし，見づらくなるので，2 行目だけ，両辺を 2 倍しておく．これは，両辺に左から

 { \displaystyle
  \begin{equation}
    \left(
    \begin{array}{ccc}
      1 & 0 & 0\\
      0 & 2 & 0\\
      0 & 0 & 1\\
    \end{array}
    \right)
  \end{equation}
}

をかけることと等しい．これで，前進消去が行えた．後は，後退代入を行っていけばよい．後退代入は，行列をもとの連立方程式の形に直したほうが分かりやすい．連立方程式の形に直すと，

 { \displaystyle
  \begin{equation}
  \left\{
    \begin{array}{cccc}
      2x_{1} & + x_{2} & - 2x_{2} & = 1\\
      & x_{2} & + 0x_{3} & = 7\\
      & & 4x_{3} & = 16\\
    \end{array}
  \right.
  \end{equation}
}

となる．ここで，あえて， {0x_{3}} を入れてある．この理由は，後々分かる．さて，後退代入は， {x_{3}, x_{2}, x_{1}} の順に計算してゆく．方程式を見ると， {x_{3} = 4} となることが直ちに分かる．次に， {x_{2}} は，以下のように式変形して求める．

 { \displaystyle
  \begin{eqnarray}
    & & x_{2} + 0 \cdot x_{3} = 7\\
    & \Leftrightarrow & x_{2} = 7 - 0 \cdot x_{3}\\
    & \Leftrightarrow & x_{2} = 7 - 0 \cdot 4\\
    & \therefore & x_{2} = 7
  \end{eqnarray}
}

この場合は， {x_{3}} の係数が 0 であったため，あまり必要性を感じないかも知れない．なので，先程と同様に {x_{1}} を計算すると，

 { \displaystyle
  \begin{eqnarray}
    & & 2x_{1} + x_{2} - 2x_{3} = 1\\
    & \Leftrightarrow & 2x_{1} = 1 - x_{2} + 2x_{3}\\
    & \Leftrightarrow & 2x_{1} = 1 - 7 + 2 \cdot 4\\
    & \Leftrightarrow & 2x_{1} = 2\\
    & \therefore & x_{1} = 1
  \end{eqnarray}
}

となる．これで，すべての解が計算できた．

アルゴリズム とサンプルプログラム

これのアルゴリズムは以下のようになる．

しかし，これでは，対角成分が 0 の場合は，計算が出来ない．そこで，ピボット選択ということを行う．これは，現在の列のうち，絶対値が最大となるものを探し，行を交換するというものである．これは，対角成分が 0 であるときの対処法だけではなく，丸め誤差の影響が小さくなる．本当は完全ピボット選択の方が良いが，プログラムを組むのが面倒なので，部分ピボット選択を行うガウスの消去法のプログラムを以下に示す．

このプログラムは，行列を 1 次元配列で確保しているので，row 行 col の行列 {A} の {(i, j)} 成分 {a_{ij}} は，A[i * col + j] となる．

参考文献

ガウスの消去法 - Wikipedia