React による WebRTC-SIP の再構築 ②通信処理
どうも,筆者です.
前回に引き続き,今度は通信処理(Communication 部分)を実装していく.
workspacememory.hatenablog.com
React による通信処理の実装
さっそく,実装していく.
ディレクトリ構成
コンポーネントに Communication.js を追加する.
.
│ docker-compose.yml
│ README.md
│ sample.env
│
└─frontend
│ Dockerfile
│ entrypoint.sh
│
├─public
│ favicon.ico
│ index.html
│ manifest.json
│ robots.txt
│
└─src
│ App.js
│ App.test.js
│ index.js
│ reportWebVitals.js
│ setupTests.js
│
├─components
│ Communication.js
│ ErrorMessage.js
│ Login.js
│
└─services
config.js
WebPhone.js
src/App.js の更新
Communication.js のコンポーネントを追加する.
import React from 'react'; import { Container, Row, Col } from 'react-bootstrap'; import ErrorMessage from './components/ErrorMessage.js'; import Login from './components/Login.js'; import Communication from './components/Communication.js'; // 追加 import webPhone from './services/WebPhone.js'; // (中略) render() { const loggedIn = this.state.loggedIn; const isLogoutProcess = this.state.isLogoutProcess; const error = this.state.error; return ( <Container> <Row> <Col> <h1>WebPhone</h1> </Col> </Row> <Login loggedIn={loggedIn} isLogoutProcess={isLogoutProcess} /> <Row> <Col> <ErrorMessage message={error} /> <hr /> </Col> </Row> <Communication loggedIn={loggedIn} /> </Container> ); // Communication を追加 }
src/Communication.js
通信処理の内容を以下に示す.
import React from 'react'; import { Row, Col, Button, FormControl } from 'react-bootstrap'; import ErrorMessage from './ErrorMessage.js'; import webPhone from '../services/WebPhone.js'; const CallMessage = (props) => { return ( <Row> <Col> <h3>{props.title}</h3> <p> <label>{props.displayType}:</label> <span>{props.displayName}</span> </p> </Col> </Row> ); }; const IncomingCall = (props) => { if (!props.isIncoming) { return null; } return ( <Row className="mt-1"> <Col> <CallMessage title={'Incoming Call'} displayType={'Incoming'} displayName={props.peerName} /> <Row className="mt-1"> <Col xs={12} lg={6}> <Button variant="success" className="btn-block" onClick={() => props.onClick(true)}> Answer </Button> </Col> <Col xs={12} lg={6}> <Button variant="danger" className="btn-block" onClick={() => props.onClick(false)}> Reject </Button> </Col> </Row> </Col> </Row> ); }; class InCall extends React.Component { constructor(props) { super(props); this.state = { isMuted: false, }; // define callback functions this.updateMuteMode = (isMuted) => { this.setState({ isMuted: isMuted, }); }; } componentDidMount() { webPhone.on('changeMuteMode', this.updateMuteMode); } componentWillUnmount() { webPhone.off('changeMuteMode', this.updateMuteMode); } render() { if (!this.props.isCalling) { return null; } const isMuted = this.state.isMuted; const variant = isMuted ? 'warning' : 'primary'; const text = isMuted ? 'Unmute (sound are muted now)' : 'Mute (sound are not muted now)'; return ( <Row className="mt-1"> <Col> <CallMessage title={'In Call'} displayType={'Peer'} displayName={this.props.peerName} /> <Row className="mt-1"> <Col> <Button variant="danger" className="btn-block" onClick={() => webPhone.hangup()}>Hangup</Button> </Col> <Col> <Button variant={variant} className="btn-block" onClick={() => webPhone.updateMuteMode()}>{text}</Button> </Col> </Row> </Col> </Row> ); } } class OutgoingCall extends React.Component { constructor(props) { super(props); this.state = { destNumber: '', errors: { destNumber: [], }, }; // define callback functions this.updateDtmf = (text) => { const value = `${this.state.destNumber}${text}`; this.setState({ destNumber: value, }); }; } componentDidMount() { webPhone.on('pushdial', this.updateDtmf); } componentWillUnmount() { webPhone.off('pushdial', this.updateDtmf); } handleChange(event) { const value = event.target.value.replace(/[^0-9*#]/g, ''); this.setState({ destNumber: value, }); } renderPad(text) { return ( <Button variant="outline-dark" className="btn-block" onClick={() => webPhone.updateDtmf(text)}> {text} </Button> ); } handleClick() { const validator = (target, message) => !target ? [message] : null; const destNumber = this.state.destNumber; this.setState({ errors: { destNumber: [], }, }); const invalidDestNumber = validator(destNumber, 'Enter the destination phone number'); if (invalidDestNumber) { this.setState({ errors: { destNumber: invalidDestNumber, }, }); return; } webPhone.call(destNumber); } handlerClear() { this.setState({ destNumber: '', }); } handleDelete() { const destNumber = this.state.destNumber; const value = destNumber.substring(0, destNumber.length - 1); this.setState({ destNumber: value, }); } render() { const isCalling = this.props.isCalling; const errors = this.state.errors; let callButton = ''; if (!isCalling) { callButton = ( <Row className='mt-3'> <Col> <Button variant="success" className="btn-block" onClick={() => this.handleClick()}> Call </Button> </Col> </Row> ); } return ( <Row className="mt-1"> <Col> <Row> <Col> <h3>Dial Pad</h3> <Row> <Col> <FormControl type="tel" name="destNumber" placeholder="enter the destination phone number" value={this.state.destNumber} onChange={(event) => this.handleChange(event)} disabled={isCalling} /> <ErrorMessage message={errors.destNumber} /> </Col> </Row> <Row className="mt-1"> <Col> <Button variant="outline-secondary" className="btn-block" onClick={() => this.handlerClear()}> Clear </Button> </Col> <Col> <Button variant="outline-danger" className="btn-block" onClick={() => this.handleDelete()}> Delete </Button> </Col> </Row> </Col> </Row> <Row className="mt-3"> <Col xs={{ span: 7, offset: 2 }} md={{ span: 4, offset: 4 }}> <Row className="no-gutters"> <Col>{this.renderPad(1)}</Col> <Col>{this.renderPad(2)}</Col> <Col>{this.renderPad(3)}</Col> </Row> <Row className="no-gutters"> <Col>{this.renderPad(4)}</Col> <Col>{this.renderPad(5)}</Col> <Col>{this.renderPad(6)}</Col> </Row> <Row className="no-gutters"> <Col>{this.renderPad(7)}</Col> <Col>{this.renderPad(8)}</Col> <Col>{this.renderPad(9)}</Col> </Row> <Row className="no-gutters"> <Col>{this.renderPad('*')}</Col> <Col>{this.renderPad(0)}</Col> <Col>{this.renderPad('#')}</Col> </Row> </Col> </Row> {callButton} </Col> </Row> ); } } class Communication extends React.Component { constructor(props) { super(props); this.callTypes = Object.freeze({ donothing: 0, incoming: 1, incall: 2, }); this.state = { callType: this.callTypes.donothing, peerName: 'Unknown', }; // define callback functions const getPeerName = (session) => { const extension = session.remote_identity.uri.user; const name = session.remote_identity.display_name; const peerName = (name) ? `${extension} (${name})` : extension; return peerName; }; this.resetSession = () => { this.setState({ callType: this.callTypes.donothing, peerName: 'Unknown', }); }; this.progress = (session) => { const peerName = getPeerName(session); const callType = (session._direction === 'incoming') ? this.callTypes.incoming : this.callTypes.incall; this.setState({ callType: callType, peerName: peerName, }); }; this.confirmed = (session) => { const peerName = getPeerName(session); this.setState({ callType: this.callTypes.incall, peerName: peerName, }); }; } componentDidMount() { webPhone.on('resetSession', this.resetSession); webPhone.on('progress', this.progress); webPhone.on('confirmed', this.confirmed); } componentWillUnmount() { webPhone.off('resetSession', this.resetSession); webPhone.off('progress', this.progress); webPhone.off('confirmed', this.confirmed); } handleIncomingCall(isAccepted) { if (isAccepted) { webPhone.answer(); this.setState({ callType: this.callTypes.incall, }); } else { webPhone.hangup(); this.setState({ callType: this.callTypes.donothing, peerName: 'Unknown', }); } } render() { if (!this.props.loggedIn) { return null; } const callType = this.state.callType; const isIncoming = callType === this.callTypes.incoming; const isCalling = callType === this.callTypes.incall; return ( <Row className="justify-content-center"> <Col> <IncomingCall isIncoming={isIncoming} peerName={this.state.peerName} onClick={(isAccepted) => this.handleIncomingCall(isAccepted)} /> <InCall isCalling={isCalling} peerName={this.state.peerName} /> <OutgoingCall isCalling={isCalling} /> </Col> </Row> ); } } export default Communication;
実装結果
実装結果を以下に格納した.必要に応じて参照して欲しい.FreePBX のサーバとアカウントがあれば利用できることを確認している.
React による WebRTC-SIP の再構築 ①ログイン処理
どうも,筆者です.
以前,JsSIP による WebRTC-SIP 環境を構築し,WebPhone を構築した. ただ,jQuery を用いていたため,変更箇所が多く,各コンポーネントの関係が複雑になっていた.
そこで,React を使って,コンポーネントベースでページを作成し,同等の機能を実現することとした.
workspacememory.hatenablog.com
制約
筆者は,React を学習し始めた初心者のため,実装が怪しい部分があり,取り敢えず動いた状態になる可能性が高い. また,今回は JsSIP によるイベント駆動のアプリケーションとの組み合わせになるため,標準的な SPA (Single Page Application) とは勝手が違う可能性もある. この辺は,今後改善していく方針とさせていただきたい.
ちなみに,筆者は,React のチュートリアルを読んで,その中で説明されている〇×ゲームのサンプルを写経した程度の準備だけしている.他の知識に関しては,都度調べながら実装している.
Docker 環境の更新
以前,React を動作させるため,Docker 環境を構築した.まずは,こちらの環境に手を加えていく.
workspacememory.hatenablog.com
docker-compose.yml
docker-compose.yml を以下のように更新した.
version: '3.4' x-logging: &json-logging driver: json-file options: max-size: "10m" max-file: "3" services: frontend: build: context: ./frontend dockerfile: Dockerfile args: TZ: "Asia/Tokyo" image: frontend.react working_dir: /home/node/app restart: always container_name: frontend-react volumes: - ./frontend/public:/home/node/app/public - ./frontend/src:/home/node/app/src - ./.env:/home/node/app/.env:ro ports: - 8888:3000 logging: *json-logging
Dockerfile
Dockerfile を以下のように更新した.
FROM node:16-alpine3.11 ARG TZ="Asia/Tokyo" ENV NODE_UID=1000 \ NODE_GID=1000 # install basic software RUN apk update \ && apk add --no-cache bash tzdata shadow su-exec tini \ && cp /usr/share/zoneinfo/${TZ} /etc/localtime \ && rm -rf /home/node/app \ && rm -rf /root/.cache /var/cache/apk/* COPY entrypoint.sh /usr/local/bin/entrypoint.sh RUN chmod +x /usr/local/bin/entrypoint.sh USER node RUN cd /home/node \ && echo -e "y\n" | npx create-react-app app -timeout=60000 \ && cd app \ && npm install react-bootstrap bootstrap@4.6.0 jssip USER root WORKDIR /home/node/app ENTRYPOINT [ "/usr/local/bin/entrypoint.sh" ] CMD [ "npm", "start" ]
entrypoint.sh
entrypoint.sh を以下のように更新した.
#!/bin/bash # get node user information uid=$(id node -u) gid=$(id node -g) # change GID if [ ${NODE_GID} -ne ${gid} ]; then groupmod -g ${NODE_GID} node fi # change UID if [ ${NODE_UID} -ne ${uid} ]; then usermod -u ${NODE_UID} node fi # update owner chown node:node package.json package-lock.json # execute process by node user exec su-exec node /sbin/tini -e 143 -- "$@"
ディレクトリ階層
ディレクトリ構造を以下のように更新した.また,デフォルトで含まれていたファイルのいくつかを削除した.
.
│ docker-compose.yml
│ README.md
│ sample.env
│
└─frontend
│ Dockerfile
│ entrypoint.sh
│
├─public
│ favicon.ico
│ index.html
│ manifest.json
│ robots.txt
│
└─src
App.js
App.test.js
index.js
reportWebVitals.js
setupTests.js
ここで,sample.evn は,React 内で用いる環境変数を設定している.実際に利用する際は,.env としてファイルを作成し,sample.env と同じ階層に配置して利用する(docker-compose.yml の volume 参照).
sample.env の構成を以下に示す.
WDS_SOCKET_PORT=0 REACT_APP_DEV_SERVER_NAME=sample.example.com REACT_APP_DEV_SIP_PORT=12345 REACT_APP_DEV_WEBSOCKET_PORT=8443 REACT_APP_DEV_BASE_URL=https://www.example.com REACT_APP_TEST_SERVER_NAME= REACT_APP_TEST_SIP_PORT= REACT_APP_TEST_WEBSOCKET_PORT= REACT_APP_TEST_BASE_URL= REACT_APP_PRODUCTION_SERVER_NAME= REACT_APP_PRODUCTION_SIP_PORT= REACT_APP_PRODUCTION_WEBSOCKET_PORT= REACT_APP_PRODUCTION_BASE_URL=
画面設計
以前の WebPhone で画面設計ができているが,React で実装する際に構築する画面構成を整理しておく.
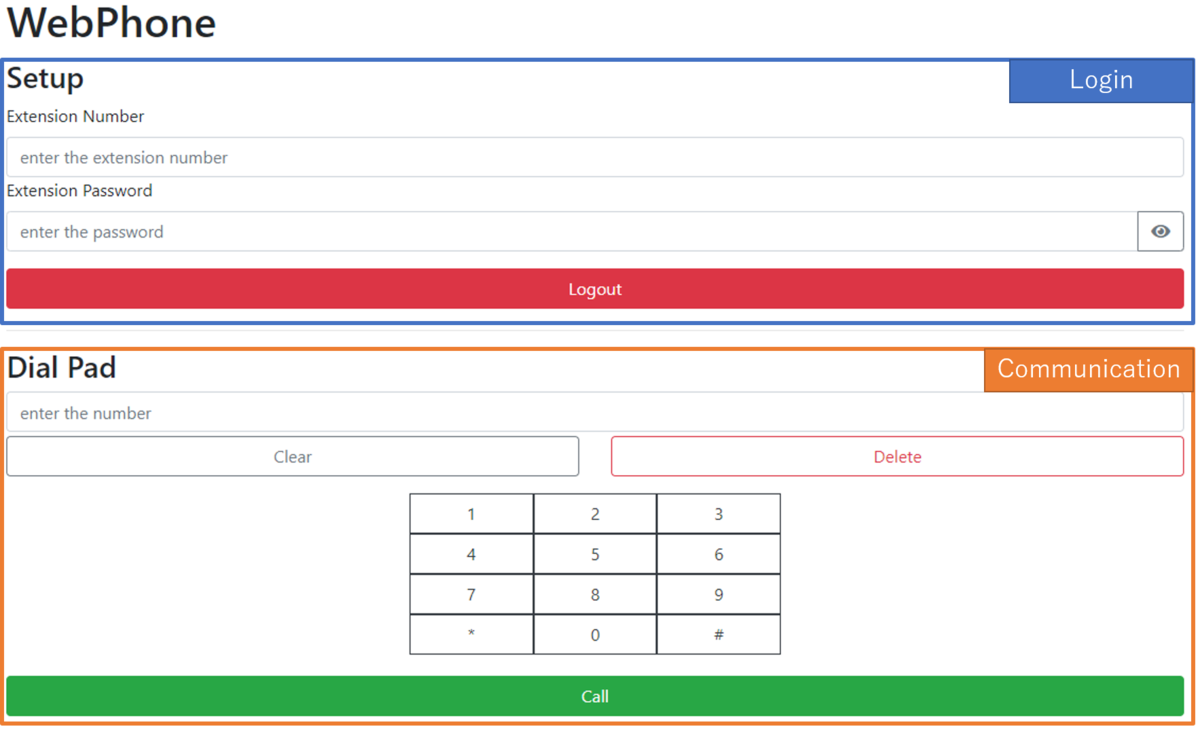
上記のように,Login 部分と Communication 部分に分けて実装予定である.このうち,今回は,Login 部分を実装する.
React によるログイン処理の実装
さっそく作り込んでいく.最終的なディレクトリ構成と各コードの内容を示していく.
ディレクトリ構成
コンポーネントと WebPhone 本体を分けて管理した.
.
│ docker-compose.yml
│ README.md
│ sample.env
│
└─frontend
│ Dockerfile
│ entrypoint.sh
│
├─public
│ favicon.ico
│ index.html
│ manifest.json
│ robots.txt
│
└─src
│ App.js
│ App.test.js
│ index.js
│ reportWebVitals.js
│ setupTests.js
│
├─components
│ ErrorMessage.js
│ Login.js
│
└─services
config.js
WebPhone.js
public/index.html
ページを表示する上で,最低限の設定が必要になる.ここでは,bootstrap を用いるので,css など必要なデータを読み込む処理も加え,html を作成している. 必要な部分は React で実装していくので,生の html をほとんど書かないというのはありがたい.
<!DOCTYPE html> <html lang="ja"> <head> <meta charset="utf-8"> <link rel="icon" href="%PUBLIC_URL%/favicon.ico" /> <meta name="viewport" content="width=device-width, initial-scale=1" /> <meta name="theme-color" content="#000000" /> <meta name="description" content="Web Phone"> <link rel="manifest" href="%PUBLIC_URL%/manifest.json" /> <link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/bootstrap@4.6.0/dist/css/bootstrap.min.css" integrity="sha384-B0vP5xmATw1+K9KRQjQERJvTumQW0nPEzvF6L/Z6nronJ3oUOFUFpCjEUQouq2+l" crossorigin="anonymous" /> <link rel="stylesheet" href="https://use.fontawesome.com/releases/v5.8.2/css/all.css" integrity="sha384-oS3vJWv+0UjzBfQzYUhtDYW+Pj2yciDJxpsK1OYPAYjqT085Qq/1cq5FLXAZQ7Ay" crossorigin="anonymous"> <title>Web Phone</title> </head> <body> <div id="root"></div> </body> </html>
src/App.js
ページの雛形となる部分である.今回は,JsSIP のログイン状態により,Communication の表示と非表示,Login ボタンのクラス設定を変更したいため,App.js でログイン状態を保持することとする. このように,ログイン状態を Login のコンポーネントに渡すことで,各コンポーネントの更新を委譲できると考えた(あっているのかなぁ...).
import React from 'react'; import { Container, Row, Col } from 'react-bootstrap'; import ErrorMessage from './components/ErrorMessage.js'; import Login from './components/Login.js'; import webPhone from './services/WebPhone.js'; class App extends React.Component { constructor(props) { super(props); this.state = { loggedIn: false, isLogoutProcess: false, error: [], }; // define callback functions const updateLoginStatus = (isEnable, err) => { const message = err ? [err] : []; this.setState({ loggedIn: isEnable, isLogoutProcess: false, error: message, }); }; this.registered = (isEnable) => { updateLoginStatus(isEnable); }; this.registrationFailed = (err, isEnable) => { updateLoginStatus(isEnable, err); }; this.logout = () => { this.setState({ isLogoutProcess: true, }); setTimeout(() => { updateLoginStatus(false); }, 3*1000); }; } componentDidMount() { webPhone.on('registered', this.registered); webPhone.on('registrationFailed', this.registrationFailed); webPhone.on('logout', this.logout); } componentWillUnmount() { webPhone.off('registered', this.registered); webPhone.off('registrationFailed', this.registrationFailed); webPhone.off('logout', this.logout); } render() { const loggedIn = this.state.loggedIn; const isLogoutProcess = this.state.isLogoutProcess; const error = this.state.error; return ( <Container> <Row> <Col> <h1>WebPhone</h1> </Col> </Row> <Login loggedIn={loggedIn} isLogoutProcess={isLogoutProcess} /> <Row> <Col> <ErrorMessage message={error} /> <hr /> </Col> </Row> </Container> ); } } export default App;
src/components/Login.js
ログイン画面に該当する部分である.こちらは,世の中のサンプルを参考に,見よう見まねで作っている.ただ,Login ボタンの class 設定「btn-block」を有効にする方法が分からなかった.ここでは,className="btn-block" として挿入している.
import React from 'react'; import { Row, Col, Button, Form, FormControl } from 'react-bootstrap'; import ErrorMessage from './ErrorMessage.js'; import webPhone from '../services/WebPhone.js'; class PasswordField extends React.Component { constructor(props) { super(props); this.state = { isVisible: false, type: 'password', }; } handleClick() { const isVisible = this.state.isVisible; this.setState({ isVisible: !isVisible, type: !isVisible ? 'text' : 'password', }); } render() { const style = { left: 'auto', position: 'absolute', right: '25px', top: '40px', }; const disabled = this.props.disabled; const type = disabled ? 'password' : this.state.type; const visibleType = (disabled || !this.state.isVisible) ? 'fas fa-eye' : 'fas fa-eye-slash'; return ( <div> <FormControl type={type} name="password" placeholder="enter the password" onChange={(event) => this.props.onChange(event)} disabled={disabled} /> <span onClick={() => this.handleClick()} style={style}> <i className={visibleType} /> </span> </div> ); } } class Login extends React.Component { constructor(props) { super(props); this.state = { username: '', password: '', errors: { username: [], password: [], }, }; } handleChange(event, converter=(val)=>val) { this.setState({ [event.target.name]: converter(event.target.value) }); } handleClick(loggedIn) { const validator = (target, message) => !target ? [message] : null; const {username, password} = this.state; this.setState({ errors: { username: [], password: [], }, }); if (this.props.loggedIn) { webPhone.logout(); } else { const invalidUsername = validator(username, 'Enter the username'); const invalidPassword = validator(password, 'Enter the password'); if (invalidUsername || invalidPassword) { this.setState({ errors: { username: invalidUsername, password: invalidPassword, }, }); return; } webPhone.login(username, password); } } render() { const loggedIn = this.props.loggedIn; const isLogoutProcess = this.props.isLogoutProcess; const text = loggedIn ? 'Logout' : 'Login'; const variant = loggedIn ? 'danger' : 'primary'; const errors = this.state.errors; return ( <Row className="justify-content-center"> <Col> <Row> <Col> <h3>Setup</h3> </Col> </Row> <Row className="mt-1"> <Col> <Form.Label>Extension Number</Form.Label> <FormControl type="tel" name="username" placeholder="enter the extension number" value={this.state.username} onChange={(event) => this.handleChange(event, (val) => val.replace(/[^0-9*#]/g, ''))} disabled={loggedIn} /> <ErrorMessage message={errors.username} /> </Col> </Row> <Row className="mt-1"> <Col> <Form.Label>Extension Password</Form.Label> <PasswordField onChange={(event) => this.handleChange(event)} disabled={loggedIn} /> <ErrorMessage message={errors.password} /> </Col> </Row> <Row className="mt-1"> <Col> <Button variant={variant} className="btn-block" onClick={() => this.handleClick()} disabled={isLogoutProcess}>{text}</Button> </Col> </Row> </Col> </Row> ); } } export default Login;
src/components/ErrorMessage.js
これまでは,エラーメッセージの表示を alert で実装していた.画面内に組み込みたかったので,世の中の記事を参考に実装した.
import React from 'react'; const ErrorMessage = (props) => { const errorStyle = { color: '#fc0101', }; const messages = props.message; return ( <React.Fragment> {(messages !== null) && messages.map((message) => <p style={errorStyle} key={message}> {message} </p> )} </React.Fragment> ); }; export default ErrorMessage;
src/services/config.js
以前は,html 内にサーバの情報などをハードコーディングしていた.これは改善したかった点の 1 つなので,今回は環境変数を用いることで回避する.
create-react-app コマンドで生成した場合,REACT_APP_ という prefix を付ければ,自動的に環境変数を読み込んでくれるらしい.これを利用し,環境変数を読み込む.
const Config = () => { const env = process.env; let ret; if (env.NODE_ENV === 'test') { // test ret = { serverName: env.REACT_APP_TEST_SERVER_NAME, sipPort: env.REACT_APP_TEST_SIP_PORT, websocketPort: env.REACT_APP_TEST_WEBSOCKET_PORT, baseUrl: env.REACT_APP_TEST_BASE_URL, }; } else if (env.NODE_ENV === 'production') { // production ret = { serverName: env.REACT_APP_PRODUCTION_SERVER_NAME, sipPort: env.REACT_APP_PRODUCTION_SIP_PORT, websocketPort: env.REACT_APP_PRODUCTION_WEBSOCKET_PORT, baseUrl: env.REACT_APP_PRODUCTION_BASE_URL, }; } else { // development ret = { serverName: env.REACT_APP_DEV_SERVER_NAME, sipPort: env.REACT_APP_DEV_SIP_PORT, websocketPort: env.REACT_APP_DEV_WEBSOCKET_PORT, baseUrl: env.REACT_APP_DEV_BASE_URL, }; } return ret; } const reactEnv = Config(); module.exports = reactEnv;
src/services/WebPhone.js
JsSIP を用いる部分の処理である.なるべく jQuery とは分離させていたため,ほぼそのまま利用できている.変更箇所のみを記載する.
import EventEmitter from 'events'; import lodash from 'lodash'; const reactEnv = require('./config.js'); const JsSIP = require('jssip'); class WebPhone extends EventEmitter { constructor() { super(); JsSIP.debug.enable('JsSIP:*'); // Setup server information →環境変数を取得し,設定するように変更 const SERVER_NAME = reactEnv.serverName; const SIP_PORT = reactEnv.sipPort; const WEBSOCKET_PORT = reactEnv.websocketPort; const baseUrl = reactEnv.baseUrl; const socket = new JsSIP.WebSocketInterface(`wss://${SERVER_NAME}:${WEBSOCKET_PORT}/ws`); const noAnswerTimeout = 15; // Time (in seconds) after which an incoming call is rejected if not answered this.sipUrl = `${SERVER_NAME}:${SIP_PORT}`; this.config = { sockets: [socket], uri: null, password: null, session_timers: false, realm: 'asterisk', display_name: null, no_answer_timeout: noAnswerTimeout, }; // (中略) // this.confirmCall を削除 // getPhoneParameter と getPhoneStatus を削除 } login(username, password) { if (this.phone) { return; } const config = Object.assign(lodash.cloneDeep(this.config), {uri: `sip:${username}@${this.sipUrl}`, password: password, display_name: username}); this.phone = new JsSIP.UA(config); // In the case of user's authentication is success this.phone.on('registered', (event) => { this.isEnable = true; this.emit('registered', this.isEnable); }); // In the case of user's authentication is failed this.phone.on('registrationFailed', (event) => { const err = `Registering on SIP server failed with error: ${event.cause}`; this.logout(); this.emit('registrationFailed', err, this.isEnable); }); // In the case of firing an incoming or outgoing session/call this.phone.on('newRTCSession', (event) => { // Reset current session const resetSession = () => { this.ringTone.pause(); this.ringTone.currentTime = 0; this.session = null; this.emit('resetSession'); }; // Enable the remote audio const addAudioTrack = () => { this.session.connection.ontrack = (ev) => { this.ringTone.pause(); this.ringTone.currentTime = 0; this.remoteAudio.srcObject = ev.streams[0]; }; }; if (this.session) { this.session.terminate(); } this.session = event.session; this.session.on('ended', resetSession); this.session.on('failed', resetSession); this.session.on('peerconnection', addAudioTrack); this.session.on('progress', () => this.emit('progress', this.session); // accept を削除し,progress を追加 this.session.on('confirmed', () => { this.ringTone.pause(); this.emit('confirmed', this.session); }); // Check the direction of this session if (this.session._direction === 'incoming') { // In the case of incoming this.ringTone.play(); // timeout 処理を削除 } else { // In the case of outgoing addAudioTrack(); } this.emit('changeMuteMode', false); // newRTCSession のイベント発火を削除 }); this.phone.start(); } logout() { if (this.phone) { this.phone.stop(); this.phone = null; this.session = null; this.lockDtmf = false; this.isEnable = false; this.emit('logout'); // event を追加 } } // (中略) } const webPhone = new WebPhone(); export default webPhone;
Reactの環境構築
どうも,筆者です.
最近,技術習得ができていないのではないかと疑問を持ち始めるようになった.ただ,仕事の都合上,自宅でできる範囲の事は限られている. そこで,Web 系の技術であれば自宅からでも勉強ができると思い立ち,Web 系の技術を学ぶこととした.
最近の流行りを追い切れていないが,以前から興味があった技術として React がある.ここでは,React を勉強し,以前作成した WebPhone の frontend を React で作り直したいと思う.(他に良い題材が無かった) React は,使ったことすらなかったので,まずは,環境を構築し,チュートリアルを進めるところまでをまとめたいと思う.構築した環境は,本番では使わない気がするが.
準備
例に漏れず,Docker で環境構築をする.まず,ディレクトリ構成は以下のようにした.public と src に関しては,コンテナ作成後,docker からホストにコピーして利用するものとする.
.
│ docker-compose.yml
│ README.md
│
└─frontend
│ Dockerfile
│ entrypoint.sh
│
├─public
│
└─src
docker-compose.yml
docker-compose.yml は以下のようになる.
version: '3.4' x-logging: &json-logging driver: json-file options: max-size: "10m" max-file: "3" services: frontend: build: context: ./frontend dockerfile: Dockerfile args: TZ: "Asia/Tokyo" image: frontend.react working_dir: /home/node/app restart: always container_name: frontend-react #volumes: # 後で,コメントを外す. # - ./frontend/public:/home/node/app/public # - ./frontend/src:/home/node/app/src ports: - 8888:3000 logging: *json-logging
Dockerfile
Dockerfile は以下のようになる.
FROM node:16-alpine3.11 ARG TZ="Asia/Tokyo" ENV NODE_UID=1000 \ NODE_GID=1000 # install basic software RUN apk update \ && apk add --no-cache bash tzdata shadow su-exec tini \ && cp /usr/share/zoneinfo/${TZ} /etc/localtime \ && mkdir -p /var/log/react \ && rm -rf /home/node/app \ && rm -rf /root/.cache /var/cache/apk/* COPY entrypoint.sh /usr/local/bin/entrypoint.sh RUN chmod +x /usr/local/bin/entrypoint.sh USER node RUN cd /home/node \ && echo -e "y\n" | npx create-react-app app \ && cd app \ && npm install log4js USER root WORKDIR /home/node/app ENTRYPOINT [ "/usr/local/bin/entrypoint.sh" ] CMD [ "npm", "start" ]
entrypoint.sh
entrypoint.sh は以下のようになる.ここでは,ホスト側の volume と共有する前提であり,root 権限でファイルが作成されないように細工している.
#!/bin/bash # get node user information uid=$(id node -u) gid=$(id node -g) # change GID if [ ${NODE_GID} -ne ${gid} ]; then groupmod -g ${NODE_GID} node fi # change UID if [ ${NODE_UID} -ne ${uid} ]; then usermod -u ${NODE_UID} node fi # update owner chown node:node /var/log/react chown node:node package.json package-lock.json # execute process by node user exec su-exec node /sbin/tini -e 143 -- "$@"
環境のビルド・生成ファイルの取得
ビルド手順と create-react-app により生成されるファイルの取得手順は,以下のようになる.
docker-compose buildにより docker image を作成する.docker-compose up -dにより,コンテナを作成する.- ホストマシンでコマンドを実行し,docker container 内のファイルをホスト側にコピーする.
docker image の作成
以下のコマンドを実行する.
docker-compose build
コンテナの作成
以下のコマンドを実行する.
docker-compose up -d # 下記のコマンドを実行し,コンテナが起動していることを確認する # docker ps -a
生成ファイルの取得
以下のコマンドを実行し,ホスト側にファイルコピーする.
# ホストマシンでコマンドを実行 # === 作業ディレクトリ === # ls # -> README.md docker-compose.yml frontend # ================== # ファイルのコピー docker cp frontend:/home/node/app/public ./frontend/public docker cp frontend:/home/node/app/src ./frontend/src # 権限の変更 sudo chown ${USER}:${USER} -R ./frontend # 階層構造の修正 mv ./frontend/public/public/* ./frontend/public mv ./frontend/src/src/* ./frontend/src rm -rf ./frontend/public/public ./frontend/src/src
この段階で,ディレクトリ構造は以下のようになる.
.
│ docker-compose.yml
│ README.md
│
└─frontend
│ Dockerfile
│ entrypoint.sh
│
├─public
│ favicon.ico
│ index.html
│ logo192.png
│ logo512.png
│ manifest.json
│ robots.txt
│
└─src
App.css
App.js
App.test.js
index.css
index.js
logo.svg
reportWebVitals.js
setupTests.js
接続確認
一度,コンテナを削除し,docker-compose.yml を更新後に,再度コンテナを作成する.
まず,以下のコマンドでコンテナを削除する.
docker-compose down
次に,コメントアウトしていた部分のコメントを外す
version: '3.4' (中略) volumes: - ./frontend/public:/home/node/app/public - ./frontend/src:/home/node/app/src (以下,省略)
再度,コンテナを作成する.
docker-compose up -d
一通り完了したら,ブラウザから http://localhost:8888 にアクセスする.
JsSIP による WebRTC-SIP の構築 その②
どうも,筆者です.
前回
前回の続きとなる.
workspacememory.hatenablog.com
動きの方を重視したいため,HTML の解説は省略する.
Javascript の実装は,大きく分けて JsSIP ライブラリを利用する部分とライブラリからのコールバックを受け,UI (User Interface) ,すなわち HTML 要素を更新する部分の 2 つがある.WebPhone クラスは,JsSIP ライブラリと UI を更新する際の薄い Wrapper となる.
WebPhone クラス
メソッド一覧
WebPhone クラスは,以下のメソッドを持つ.
login
ユーザ名(ここでは内線番号)とパスワードを受け取り,ログイン処理を実施する.
logout
ログアウト処理を実施する.
call
電話をかける処理を実施する.事前にログイン処理を済ませ,ユーザ認証が完了していないと利用できない.
answer
着信に応答する.事前にログイン処理を済ませ,ユーザ認証が完了していないと着信しない.
hangup
電話を切る.
updateMuteMode
ミュートオン/オフの状態を変更する.デフォルトはミュートオフ.
updateDtmf
ダイアル時の押下音を鳴らす.押下音は,変更可能.
getPhoneParameter
UI を更新する際に渡すパラメータを定義する.
getPhoneStatus
WebPhone の利用可否を返す.true の場合は利用可,false の場合は利用不可.
コンストラクタ
ここでは,JsSIP ライブラリを用いて,PBX サーバと通信するための初期設定を行う.PBX サーバは,Asterisk を利用している想定とする.
constructor() { // EventEmitter を利用するため,親クラスのコンストラクタを呼び出す super(); // デバッグ用のログ出力 JsSIP.debug.enable('JsSIP:*'); // // Setup server information // // 接続先のサーバ名 const SERVER_NAME = 'sample.example.com'; // SIP 通信時のポート番号(Asterisk の設定に合わせる) const SIP_PORT = 12345; // WebSocket を利用する際のポート番号(Asterisk の設定に合わせる) const WEBSOCKET_PORT = 8443; // 音声ファイル指定用の URL(自身の環境に合わせる) const baseUrl = `${location.protocol}//${location.host}`; // WebSocket の作成(接続先は,自身の環境に合わせる) const socket = new JsSIP.WebSocketInterface(`wss://${SERVER_NAME}:${WEBSOCKET_PORT}/ws`); // SIP サーバの URL(接続先は,自身の環境に合わせる) this.sipUrl = `${SERVER_NAME}:${SIP_PORT}`; this.config = { sockets: [socket], uri: null, password: null, session_timers: false, realm: 'asterisk', display_name: null, }; this.callOptions = { mediaConstraints: { audio: true, video: false }, // ここでは,音声のみを利用可能とする }; // 応答なしと判断する際の時間(sec) this.noAnswerTimeout = 15; // 着信音.ファイルは自前で用意し,サーバに配置すること. this.ringTone = new window.Audio(`${baseUrl}/audio/ringtone.mp3`); // ダイアル時のプッシュ音.ファイルは自前で用意し,サーバに配置すること. this.dtmfTone = new window.Audio(`${baseUrl}/audio/dtmf.wav`); this.ringTone.loop = true; this.remoteAudio = new Audio(); this.remoteAudio.autoplay = true; // クラス内変数の初期化 this.phone = null; this.session = null; this.confirmCall = false; this.lockDtmf = false; this.isEnable = false; this.dtmfTone.onended = () => { this.lockDtmf = false }; // bind this.login = this.login.bind(this); this.logout = this.logout.bind(this); this.call = this.call.bind(this); this.answer = this.answer.bind(this); this.hangup = this.hangup.bind(this); this.updateMuteMode = this.updateMuteMode.bind(this); this.updateDtmf = this.updateDtmf.bind(this); this.getPhoneParameter = this.getPhoneParameter.bind(this); this.getPhoneStatus = this.getPhoneStatus.bind(this); }
login メソッド
ユーザ名(ここでは,内線番号)とパスワードを用いて,ログイン処理を行う.ログイン処理に成功すると,着信可能状態となる.ログイン処理に失敗するとログアウト処理を行う.どちらの場合も,イベントが発火する.
login(username, password) { // username: ログインユーザ名(ここでは,内線番号) // password: パスワード // 既にインスタンスが生成されている場合は,何もせずに抜ける if (this.phone) { return; } // 既存の config をベースに,uri, display_name を設定し,SIP 通信用のインスタンスを生成 const config = $.extend(true, $.extend(true, {}, this.config), { uri: `sip:${username}@${this.sipUrl}`, password: password, display_name: username }); this.phone = new JsSIP.UA(config); // In the case of user's authentication is success this.phone.on('registered', (event) => { // ログインに成功した場合,状態を更新し,イベントを発火させる this.isEnable = true; this.emit('registered', this.getPhoneParameter()); }); // In the case of user's authentication is failed this.phone.on('registrationFailed', (event) => { // ログインに失敗した場合,ログアウト処理を行い,イベントを発火させる const err = `Registering on SIP server failed with error: ${event.cause}`; this.logout(); this.emit('registrationFailed', err, this.getPhoneParameter()); }); // In the case of firing an incoming or outgoing session/call this.phone.on('newRTCSession', (event) => { // Reset current session const resetSession = () => { // 発信者が hangup した場合を考慮し,着信音を停止 this.ringTone.pause(); this.ringTone.currentTime = 0; // 現在の session を破棄し,イベントを発火させる this.session = null; this.emit('resetSession', this.getPhoneParameter()); }; // Enable the remote audio const addAudioTrack = () => { // 音声通信用に callback を設定 this.session.connection.ontrack = (ev) => { // 着信音を停止し,通話相手の音声が発信者側に届くように設定 this.ringTone.pause(); this.ringTone.currentTime = 0; this.remoteAudio.srcObject = ev.streams[0]; }; }; // 前回の session が残っている場合は破棄 if (this.session) { this.session.terminate(); } // 確立した session を取得 this.session = event.session; // イベント発火時の callback を設定 this.session.on('ended', resetSession); this.session.on('failed', resetSession); this.session.on('accepted', () => this.emit('accepted', this.getPhoneParameter())); this.session.on('peerconnection', addAudioTrack); this.session.on('confirmed', () => this.emit('confirmed', this.getPhoneParameter())); // Check the direction of this session if (this.session._direction === 'incoming') { // 着信時に着信音を再生.TimeOut 用の処理を定義 // In the case of incoming this.ringTone.play(); this.confirmCall = setTimeout(() => { this.hangup(); this.emit('noanswer', this.getPhoneParameter()); }, this.noAnswerTimeOut * 1000); } else { // 発信後,相手の音声を再生できるように設定内容を更新 // In the case of outgoing addAudioTrack(); } // イベント発火 this.emit('newRTCSession', this.getPhoneParameter()); this.emit('changeMuteMode', false); }); this.phone.start(); }
logout メソッド
logout() { // インスタンスが生成されている場合のみ処理を実施 if (this.phone) { this.phone.stop(); // 使用済みの変数をリセット this.phone = null; this.session = null; this.confirmCall = false; this.lockDtmf = false; this.isEnable = false; } }
call メソッド
call(destNum) { // destNum: 発信先の内線番号 // インスタンスが生成されている場合のみ処理を実施 if (this.phone) { // 事前に設定した callOption を指定し,引数で受け取った番号に電話をかける this.phone.call(destNum, this.callOptions); } }
answer メソッド
answer() { // session が確立している場合のみ処理を実施 if (this.session) { // 着信に応答 this.session.answer(this.callOptions); // TimeOut 用の callback 関数が定義されている場合は,リセット処理を実施 if (this.confirmCall) { clearTimeout(this.confirmCall); this.confirmCall = false; } } }
hangup メソッド
hangup() { // session が確立している場合のみ処理を実施 if (this.session) { // 着信音を止め,セッションを中断 this.ringTone.pause(); this.ringTone.currentTime = 0; this.session.terminate(); } }
updateMuteMode メソッド
updateMuteMode() { // session が確立している場合のみ処理を実施 if (this.session) { const isMuted = this.session.isMuted().audio; // 現在の mute 状態をもとに,状態を更新 if (isMuted) { this.session.unmute({audio: true}); } else { this.session.mute({audio: true}); } // イベントを発火させる this.emit('changeMuteMode', !isMuted); } }
updateDtmf メソッド
updateDtmf(text) { // text: 押下したダイアル番号(「*」と「#」を含む) // ダイアル時の押下音が再生されていないときのみ処理を実施 if (!this.lockDtmf) { this.lockDtmf = true; this.dtmfTone.play(); // session が確立しているときは,押下した番号を送信 if (this.session) { this.session.sendDTMF(text); } // イベントを発火させる this.emit('pushdial', text); } }
getPhoneParameter メソッド
getPhoneParameter() { // 公開するパラメータの設定 const ret = { session: this.session, ringTone: this.ringTone, isEnable: this.isEnable, }; return ret; }
getPhoneStatus メソッド
getPhoneStatus() { // WebPhone の状態を返却 return this.isEnable; }
ログイン状態の更新
ログイン状態に応じて,HTML 要素を更新する関数を以下に示す.
const updateLoginStatus = (isEnable) => { const element = $('#login-status'); // ログイン状態に応じて,ボタン名やデザインを更新 if (isEnable) { element.text('Logout'); element.removeClass('btn-primary'); element.addClass('btn-danger'); } else { element.text('Login'); element.addClass('btn-primary'); element.removeClass('btn-danger'); } };
init 関数
初期化処理を行う.
User Interface の更新
着信時と発信時の状態に合わせ,表示する HTML 要素を制御する.
// User Interface の更新 const updateCallUI = (callType) => { const answer = $('#answer'); const hangup = $('#hangup'); const reject = $('#reject'); const muteMode = $('#mute-mode'); const call = $('#call'); // 着信時の処理 // In the case of incoming if (callType === 'incoming') { // hide hangup.hide(); hangup.prop('disabled', true); muteMode.hide(); muteMode.prop('disabled', true); // show answer.show(); answer.prop('disabled', false); reject.show(); reject.prop('disabled', false); } // 発信時の処理 // In the case of outgoing or busy else { // hide answer.hide(); answer.prop('disabled', true); reject.hide(); reject.prop('disabled', true); // show hangup.show(); hangup.prop('disabled', false); muteMode.show(); muteMode.prop('disabled', false); } // 共通処理 call.hide(); call.prop('disabled', true); };
WebPhone インスタンスの生成
// Create Web Phone instance const webPhone = new WebPhone();
WebPhone によるイベント発火時の callback の登録
// ここでの引数 params の内容は,getPhoneParameter メソッドを参照のこと webPhone.on('registered', (params) => { // ログイン状態を更新 updateLoginStatus(params.isEnable); $('#wrapper').show(); $('#incoming-call').hide(); $('#call-status').hide(); $('#dial-field').show(); $('#call').show(); $('#call').prop('disabled', false); $('#hangup').hide(); $('#hangup').prop('disabled', true); $('#mute-mode').hide(); $('#mute-mode').prop('disabled', true); $('#to-field').focus(); }); webPhone.on('registrationFailed', (err, params) => { // err: エラーメッセージ $('#wrapper').hide(); // ログイン状態を更新 updateLoginStatus(params.isEnable); console.log(err); // エラーメッセージの内容をアラートで示す alert(err); }); webPhone.on('resetSession', (params) => { $('#wrapper').show(); $('#incoming-call').hide(); $('#call-status').hide(); $('#dial-field').show(); $('#call').show(); $('#call').prop('disabled', false); $('#hangup').hide(); $('#hangup').prop('disabled', true); $('#mute-mode').hide(); $('#mute-mode').prop('disabled', true); }); webPhone.on('accepted', () => {return;}); webPhone.on('confirmed', (params) => { const session = params.session; if (session.isEstablished()) { const extension = session.remote_identity.uri.user; const name = session.remote_identity.display_name; const infoNumber = (name) ? `${extension} (${name})` : extension; $('#incoming-call').hide(); $('#incoming-call-number').html(''); $('#call-info-text').html('In Call'); $('#call-info-number').html(infoNumber); $('#call-status').show(); $('#dial-field').show(); params.ringTone.pause(); updateCallUI('busy'); } }); webPhone.on('newRTCSession', (params) => { const session = params.session; if (session.isInProgress()) { const extension = session.remote_identity.uri.user; const name = session.remote_identity.display_name; const infoNumber = (name) ? `${extension} (${name})` : extension; if (session._direction === 'incoming') { $('#incoming-call').show(); $('#incoming-call-number').html(infoNumber); $('#call-status').hide(); updateCallUI('incoming'); } else { $('#incoming-call').hide(); $('#incoming-call-number').html(''); $('#call-info-text').html('Ringing...'); $('#call-info-number').html(infoNumber); $('#call-status').show(); updateCallUI('outgoing'); } } }); webPhone.on('noanswer', (params) => { $('#incoming-call-number').html('Unknown'); $('#call-info-text').html('No Answer'); $('#call-info-number').html('Unknown'); }); webPhone.on('changeMuteMode', (isMuted) => { const muteMode = $('#mute-mode'); if (isMuted) { muteMode.text('Unmute (sound are muted now)'); muteMode.addClass('btn-warning'); muteMode.removeClass('btn-primary'); } else { muteMode.text('Mute (sound are not muted now)'); muteMode.removeClass('btn-warning'); muteMode.addClass('btn-primary'); } }); webPhone.on('pushdial', (text) => { const toField = $('#to-field'); const fieldValue = toField.val(); toField.val(fieldValue + text); });
HTML 要素に関するイベント発火時の callback の登録
// 要素内で Enter キー押下時の処理 const chkEnterKey = (event, element) => { if (event.key === 'Enter') { element.click(); } }; // ユーザ名(ここでは,内線番号)とパスワードの入力欄に対する設定 $('#extension-number').focus(); $('#extension-number').keyup((event) => chkEnterKey(event, $('#login-status'))); $('#extension-password').keyup((event) => chkEnterKey(event, $('#login-status'))); // ログインボタン押下時の処理 $('#login-status').click((event) => { const validator = (username, password) => { const judge = (val) => !val || !val.match(/\S/g); if (judge(username) || !/\d+/.test(username)) { throw new Error('Invalid Extension Number'); } if (judge(password)) { throw new Error('Invalid Extension Password'); } }; if (webPhone.getPhoneStatus()) { webPhone.logout(); $('#wrapper').hide(); updateLoginStatus(false); } else { const username = $('#extension-number').val(); const password = $('#extension-password').val(); try { validator(username, password); webPhone.login(username, password); } catch (err) { alert(err.message); } } }); // ダイアルパッド押下時の処理 $('.dialpad-btn').click((event) => { const text = $(event.currentTarget).text(); webPhone.updateDtmf(text); }); // clear ボタン,delete ボタン押下時の処理 $('#clear-field').click((event) => { const toField = $('#to-field'); toField.val(''); }); $('#delete-field').click((event) => { const toField = $('#to-field'); const fieldValue = toField.val(); toField.val(fieldValue.substring(0, fieldValue.length - 1)); }); // call ボタン,answer ボタン,hangup ボタン,reject ボタン,mute ボタン押下時の処理 $('#call').click(() => { const destNum = $('#to-field').val(); webPhone.call(destNum); }); $('#answer').click(webPhone.answer); $('#hangup').click(webPhone.hangup); $('#reject').click(webPhone.hangup); $('#mute-mode').click(webPhone.updateMuteMode); // 発信番号記入欄に関する設定 $('#to-field').keyup((event) => chkEnterKey(event, $('#call'))); $('#to-field').keypress((event) => { const value = String.fromCharCode(event.which); const ret = /[0-9\*#]/.test(value); return ret; }); $('#to-field').change((event) => { const element = $(event.currentTarget); const value = element.val(); element.val(value.replace(/[^0-9\*#]/g, '')); });
JsSIP による WebRTC-SIP の構築 その①
どうも,筆者です.
以前,FreePBX で IP 電話の環境を構築した.その際に,UCP(User Control Panel) と WebPhone というモジュールを追加した. しかし,スマホで UCP の WebPhone が利用できなかったため,自分で WebRTC-SIP を構築することとした.また,ここでは,JsSIP ライブラリを用いることとした.
参考サイト
外観
ログインしたときの見え方を以下に示す.あまり凝った作りにしていないため,見た目は悪い.
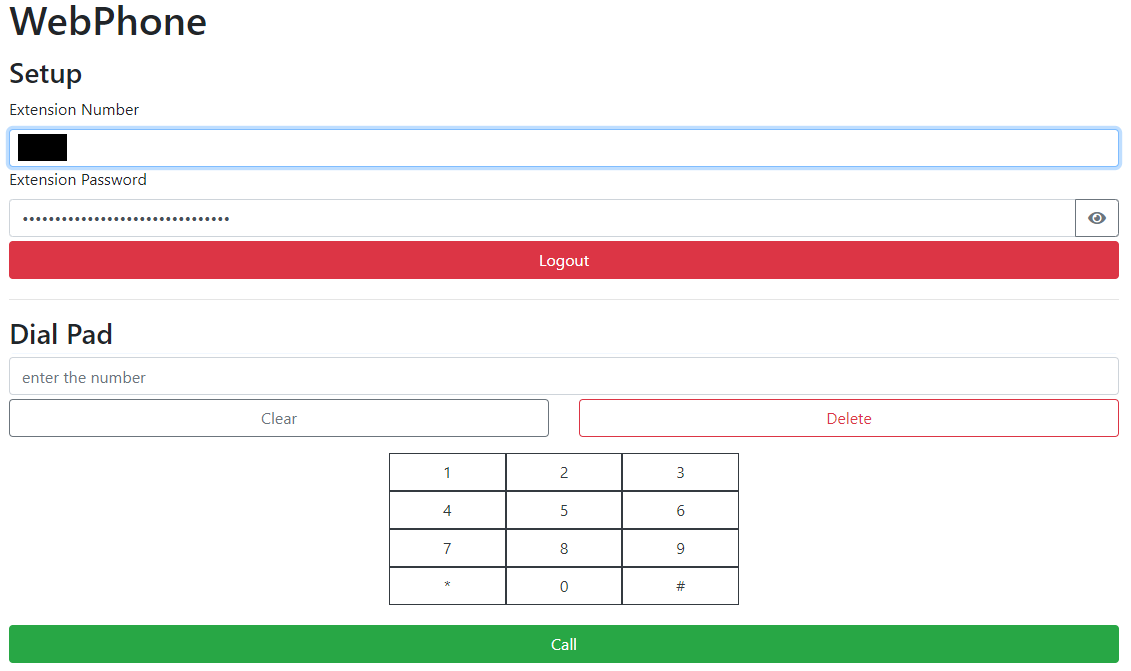
実装
ここでは,SPA(Single Page Application) として実装している.見栄えの関係上,HTML 部分と Javascript 部分を分けて示す.
HTML部分
<!DOCTYPE html> <html lang="ja"> <head> <meta charset="utf-8"> <meta name="description" content="WebRTC"> <meta name="auther" content="freepbx"> <meta name="viewport" content="width=device-width, initial-scale=1, shrink-to-fit=no"> <link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/bootstrap@4.6.0/dist/css/bootstrap.min.css" integrity="sha384-B0vP5xmATw1+K9KRQjQERJvTumQW0nPEzvF6L/Z6nronJ3oUOFUFpCjEUQouq2+l" crossorigin="anonymous"> <link rel="stylesheet" href="https://cdn.jsdelivr.net/gh/gitbrent/bootstrap4-toggle@3.6.1/css/bootstrap4-toggle.min.css"> <link rel="stylesheet" href="https://use.fontawesome.com/releases/v5.8.2/css/all.css" integrity="sha384-oS3vJWv+0UjzBfQzYUhtDYW+Pj2yciDJxpsK1OYPAYjqT085Qq/1cq5FLXAZQ7Ay" crossorigin="anonymous"> <link rel="icon" type="image/png" href="/favicon.ico"> <title>WebPhone</title> <style> .dialpad-btn { border-radius: 0px; } </style> </head> <body> <div class="container"> <div class="row justify-content-center mt-1"> <div class="col-12"> <h1 class="h1">WebPhone</h1> </div> </div> <div class="row justify-content-center mt-1"> <div class="col-12"> <div class="row"> <div class="col-12"> <h3 class="h3">Setup</h3> </div> </div> <div class="row"> <div class="col-12"> <label>Extension Number</label> <input type="tel" class="form-control" id="extension-number" placeholder="enter the extension number"> </div> </div> <div class="row"> <div class="col-12"> <label>Extension Password</label> <input type="password" class="form-control" data-toggle="password" id="extension-password" placeholder="enter the password"> </div> </div> <div class="row mt-1"> <div class="col-12"> <button type="button" id="login-status" class="btn btn-primary btn-block">Login</button> </div> </div> </div> </div> <div class="row justify-content-center mt-1"> <div class="col-12"> <div id="wrapper"> <!-- Incoming Call --> <div class="row"> <div class="col-12"> <div id="incoming-call" style="display: none;"> <hr> <div class="row"> <div class="col-12"> <h3 class="h3">Incoming Call</h3> <p> <label>Incoming:</label> <span id="incoming-call-number">Unknown</span> </p> </div> </div> <div class="row mt-1"> <div class="col-12 col-lg-6"> <button type="button" id="answer" class="btn btn-success btn-block">Answer</button> </div> <div class="col-12 col-lg-6"> <button type="button" id="reject" class="btn btn-danger btn-block">Reject</button> </div> </div> </div> <div id="call-status" style="display: none;"> <div class="row"> <div class="col-12"> <h5 class="h5" id="call-info-text">info text goes here</h5> <p> <label>Peer:</label> <span id="call-info-number">info number goes here</span> </p> </div> </div> </div> </div> </div> <!-- Dial Field --> <div class="row"> <div class="col-12"> <div id="dial-field" style="display: none;"> <hr> <!-- To Field --> <div class="row"> <div class="col-12"> <h3 class="h3">Dial Pad</h3> <div class="row"> <div class="col-12"> <input type="tel" id="to-field" class="form-control" placeholder="enter the number"> </div> </div> </div> </div> <div class="row mt-1"> <div class="col-12 col-lg-6"> <button type="button" id="clear-field" class="btn btn-outline-secondary btn-block">Clear</button> </div> <div class="col-12 col-lg-6"> <button type="button" id="delete-field" class="btn btn-outline-danger btn-block">Delete</button> </div> </div> <!-- Dial Pad --> <div class="row mt-3"> <div class="col-7 offset-2 col-md-4 offset-md-4"> <div class="row no-gutters"> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">1</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">2</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">3</button></div> </div> <div class="row no-gutters"> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">4</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">5</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">6</button></div> </div> <div class="row no-gutters"> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">7</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">8</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">9</button></div> </div> <div class="row no-gutters"> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">*</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">0</button></div> <div class="col-4"><button type="button" class="btn btn-outline-dark btn-block dialpad-btn">#</button></div> </div> </div> </div> <div class="row mt-3"> <div class="col-12"> <div class="row mt-1"> <div class="col-12"> <button type="button" id="call" class="btn btn-success btn-block">Call</button> </div> </div> <div class="row mt-1"> <div class="col-12 col-lg-6"> <button type="button" id="hangup" class="btn btn-danger btn-block">Hangup</button> </div> <div class="col-12 col-lg-6"> <button type="button" id="mute-mode" class="btn btn-primary btn-block">Mute (sound are not muted now)</button> </div> </div> </div> </div> </div> </div> </div> </div> </div> </div> </div> <script src="https://cdnjs.cloudflare.com/ajax/libs/jquery/3.5.1/jquery.min.js" integrity="sha512-bLT0Qm9VnAYZDflyKcBaQ2gg0hSYNQrJ8RilYldYQ1FxQYoCLtUjuuRuZo+fjqhx/qtq/1itJ0C2ejDxltZVFg==" crossorigin="anonymous"></script> <script src="https://cdn.jsdelivr.net/npm/bootstrap@4.6.0/dist/js/bootstrap.bundle.min.js" integrity="sha384-Piv4xVNRyMGpqkS2by6br4gNJ7DXjqk09RmUpJ8jgGtD7zP9yug3goQfGII0yAns" crossorigin="anonymous"></script> <script src="https://cdn.jsdelivr.net/gh/gitbrent/bootstrap4-toggle@3.6.1/js/bootstrap4-toggle.min.js"></script> <script src="https://cdnjs.cloudflare.com/ajax/libs/jssip/3.1.2/jssip.js" integrity="sha512-QWvPQCHjnZ9MksHgz1GRkjRVuj+BJZIV/3fBvFOs7N99N2dBaeHesIQ/+52jJOLowS2JLU6fGjQZFJfIzzFN7A==" crossorigin="anonymous" referrerpolicy="no-referrer"></script> <script src="https://unpkg.com/bootstrap-show-password@1.2.1/dist/bootstrap-show-password.min.js"></script> <script src="https://cdnjs.cloudflare.com/ajax/libs/EventEmitter/5.2.8/EventEmitter.min.js" integrity="sha512-AbgDRHOu/IQcXzZZ6WrOliwI8umwOgLE7sZgRAsNzmcOWlQA8RhXQzBx99Ho0jlGPWIPoT9pwk4kmeeR4qsV/g==" crossorigin="anonymous" referrerpolicy="no-referrer"></script> <script> (function () { // Javascript 部分に示す }()); </script> </body> </html>
Javascript 部分
class WebPhone extends EventEmitter { constructor() { super(); JsSIP.debug.enable('JsSIP:*'); // Setup server information const SERVER_NAME = 'sample.example.com'; const SIP_PORT = 12345; const WEBSOCKET_PORT = 8443; const baseUrl = `${location.protocol}//${location.host}`; const socket = new JsSIP.WebSocketInterface(`wss://${SERVER_NAME}:${WEBSOCKET_PORT}/ws`); this.sipUrl = `${SERVER_NAME}:${SIP_PORT}`; this.config = { sockets: [socket], uri: null, password: null, session_timers: false, realm: 'asterisk', display_name: null, }; this.callOptions = { mediaConstraints: {audio: true, video: false}, }; this.noAnswerTimeout = 15; // Time (in seconds) after which an incoming call is rejected if not answered this.ringTone = new window.Audio(`${baseUrl}/audio/ringtone.mp3`); this.dtmfTone = new window.Audio(`${baseUrl}/audio/dtmf.wav`); this.ringTone.loop = true; this.remoteAudio = new Audio(); this.remoteAudio.autoplay = true; this.phone = null; this.session = null; this.confirmCall = false; this.lockDtmf = false; this.isEnable = false; this.dtmfTone.onended = () => {this.lockDtmf = false}; // bind this.login = this.login.bind(this); this.logout = this.logout.bind(this); this.call = this.call.bind(this); this.answer = this.answer.bind(this); this.hangup = this.hangup.bind(this); this.updateMuteMode = this.updateMuteMode.bind(this); this.updateDtmf = this.updateDtmf.bind(this); this.getPhoneParameter = this.getPhoneParameter.bind(this); this.getPhoneStatus = this.getPhoneStatus.bind(this); } login(username, password) { if (this.phone) { return; } const config = $.extend(true, $.extend(true, {}, this.config), {uri: `sip:${username}@${this.sipUrl}`, password: password, display_name: username}); this.phone = new JsSIP.UA(config); // In the case of user's authentication is success this.phone.on('registered', (event) => { this.isEnable = true; this.emit('registered', this.getPhoneParameter()); }); // In the case of user's authentication is failed this.phone.on('registrationFailed', (event) => { const err = `Registering on SIP server failed with error: ${event.cause}`; this.logout(); this.emit('registrationFailed', err, this.getPhoneParameter()); }); // In the case of firing an incoming or outgoing session/call this.phone.on('newRTCSession', (event) => { // Reset current session const resetSession = () => { this.ringTone.pause(); this.ringTone.currentTime = 0; this.session = null; this.emit('resetSession', this.getPhoneParameter()); }; // Enable the remote audio const addAudioTrack = () => { this.session.connection.ontrack = (ev) => { this.ringTone.pause(); this.ringTone.currentTime = 0; this.remoteAudio.srcObject = ev.streams[0]; }; }; if (this.session) { this.session.terminate(); } this.session = event.session; this.session.on('ended', resetSession); this.session.on('failed', resetSession); this.session.on('accepted', () => this.emit('accepted', this.getPhoneParameter())); this.session.on('peerconnection', addAudioTrack); this.session.on('confirmed', () => this.emit('confirmed', this.getPhoneParameter())); // Check the direction of this session if (this.session._direction === 'incoming') { // In the case of incoming this.ringTone.play(); this.confirmCall = setTimeout(() => { this.hangup(); this.emit('noanswer', this.getPhoneParameter()); }, this.noAnswerTimeOut * 1000); } else { // In the case of outgoing addAudioTrack(); } this.emit('newRTCSession', this.getPhoneParameter()); this.emit('changeMuteMode', false); }); this.phone.start(); } logout() { if (this.phone) { this.phone.stop(); this.phone = null; this.session = null; this.confirmCall = false; this.lockDtmf = false; this.isEnable = false; } } call(destNum) { if (this.phone) { this.phone.call(destNum, this.callOptions); } } answer() { if (this.session) { this.session.answer(this.callOptions); if (this.confirmCall) { clearTimeout(this.confirmCall); this.confirmCall = false; } } } hangup() { if (this.session) { this.ringTone.pause(); this.ringTone.currentTime = 0; this.session.terminate(); } } updateMuteMode() { if (this.session) { const isMuted = this.session.isMuted().audio; if (isMuted) { this.session.unmute({audio: true}); } else { this.session.mute({audio: true}); } this.emit('changeMuteMode', !isMuted); } } updateDtmf(text) { if (!this.lockDtmf) { this.lockDtmf = true; this.dtmfTone.play(); if (this.session) { this.session.sendDTMF(text); } this.emit('pushdial', text); } } getPhoneParameter() { const ret = { session: this.session, ringTone: this.ringTone, isEnable: this.isEnable, }; return ret; } getPhoneStatus() { return this.isEnable; } } // Update Login Status const updateLoginStatus = (isEnable) => { const element = $('#login-status'); if (isEnable) { element.text('Logout'); element.removeClass('btn-primary'); element.addClass('btn-danger'); } else { element.text('Login'); element.addClass('btn-primary'); element.removeClass('btn-danger'); } }; const init = () => { const updateCallUI = (callType) => { const answer = $('#answer'); const hangup = $('#hangup'); const reject = $('#reject'); const muteMode = $('#mute-mode'); const call = $('#call'); // In the case of incoming if (callType === 'incoming') { // hide hangup.hide(); hangup.prop('disabled', true); muteMode.hide(); muteMode.prop('disabled', true); // show answer.show(); answer.prop('disabled', false); reject.show(); reject.prop('disabled', false); } // In the case of outgoing or busy else { // hide answer.hide(); answer.prop('disabled', true); reject.hide(); reject.prop('disabled', true); // show hangup.show(); hangup.prop('disabled', false); muteMode.show(); muteMode.prop('disabled', false); } call.hide(); call.prop('disabled', true); }; // Create Web Phone instance const webPhone = new WebPhone(); // Register callback functions webPhone.on('registered', (params) => { updateLoginStatus(params.isEnable); $('#wrapper').show(); $('#incoming-call').hide(); $('#call-status').hide(); $('#dial-field').show(); $('#call').show(); $('#call').prop('disabled', false); $('#hangup').hide(); $('#hangup').prop('disabled', true); $('#mute-mode').hide(); $('#mute-mode').prop('disabled', true); $('#to-field').focus(); }); webPhone.on('registrationFailed', (err, params) => { $('#wrapper').hide(); updateLoginStatus(params.isEnable); console.log(err); alert(err); }); webPhone.on('resetSession', (params) => { $('#wrapper').show(); $('#incoming-call').hide(); $('#call-status').hide(); $('#dial-field').show(); $('#call').show(); $('#call').prop('disabled', false); $('#hangup').hide(); $('#hangup').prop('disabled', true); $('#mute-mode').hide(); $('#mute-mode').prop('disabled', true); }); webPhone.on('accepted', () => {return;}); webPhone.on('confirmed', (params) => { const session = params.session; if (session.isEstablished()) { const extension = session.remote_identity.uri.user; const name = session.remote_identity.display_name; const infoNumber = (name) ? `${extension} (${name})` : extension; $('#incoming-call').hide(); $('#incoming-call-number').html(''); $('#call-info-text').html('In Call'); $('#call-info-number').html(infoNumber); $('#call-status').show(); $('#dial-field').show(); params.ringTone.pause(); updateCallUI('busy'); } }); webPhone.on('newRTCSession', (params) => { const session = params.session; if (session.isInProgress()) { const extension = session.remote_identity.uri.user; const name = session.remote_identity.display_name; const infoNumber = (name) ? `${extension} (${name})` : extension; if (session._direction === 'incoming') { $('#incoming-call').show(); $('#incoming-call-number').html(infoNumber); $('#call-status').hide(); updateCallUI('incoming'); } else { $('#incoming-call').hide(); $('#incoming-call-number').html(''); $('#call-info-text').html('Ringing...'); $('#call-info-number').html(infoNumber); $('#call-status').show(); updateCallUI('outgoing'); } } }); webPhone.on('noanswer', (params) => { $('#incoming-call-number').html('Unknown'); $('#call-info-text').html('No Answer'); $('#call-info-number').html('Unknown'); }); webPhone.on('changeMuteMode', (isMuted) => { const muteMode = $('#mute-mode'); if (isMuted) { muteMode.text('Unmute (sound are muted now)'); muteMode.addClass('btn-warning'); muteMode.removeClass('btn-primary'); } else { muteMode.text('Mute (sound are not muted now)'); muteMode.removeClass('btn-warning'); muteMode.addClass('btn-primary'); } }); webPhone.on('pushdial', (text) => { const toField = $('#to-field'); const fieldValue = toField.val(); toField.val(fieldValue + text); }); // Register callback functions of html elements const chkEnterKey = (event, element) => { if (event.key === 'Enter') { element.click(); } }; $('#extension-number').focus(); $('#extension-number').keyup((event) => chkEnterKey(event, $('#login-status'))); $('#extension-password').keyup((event) => chkEnterKey(event, $('#login-status'))); $('#login-status').click((event) => { const validator = (username, password) => { const judge = (val) => !val || !val.match(/\S/g); if (judge(username) || !/\d+/.test(username)) { throw new Error('Invalid Extension Number'); } if (judge(password)) { throw new Error('Invalid Extension Password'); } }; if (webPhone.getPhoneStatus()) { webPhone.logout(); $('#wrapper').hide(); updateLoginStatus(false); } else { const username = $('#extension-number').val(); const password = $('#extension-password').val(); try { validator(username, password); webPhone.login(username, password); } catch (err) { alert(err.message); } } }); $('.dialpad-btn').click((event) => { const text = $(event.currentTarget).text(); webPhone.updateDtmf(text); }); $('#clear-field').click((event) => { const toField = $('#to-field'); toField.val(''); }); $('#delete-field').click((event) => { const toField = $('#to-field'); const fieldValue = toField.val(); toField.val(fieldValue.substring(0, fieldValue.length - 1)); }); $('#call').click(() => { const destNum = $('#to-field').val(); webPhone.call(destNum); }); $('#answer').click(webPhone.answer); $('#hangup').click(webPhone.hangup); $('#reject').click(webPhone.hangup); $('#mute-mode').click(webPhone.updateMuteMode); $('#to-field').keyup((event) => chkEnterKey(event, $('#call'))); $('#to-field').keypress((event) => { const value = String.fromCharCode(event.which); const ret = /[0-9\*#]/.test(value); return ret; }); $('#to-field').change((event) => { const element = $(event.currentTarget); const value = element.val(); element.val(value.replace(/[^0-9\*#]/g, '')); }); }; $(init);
詳細
実装内容の詳細に関しては,その②で説明する.